円 面積 積分 107476

高校生向け 積分 円の面積 Youtube

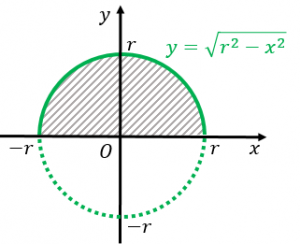
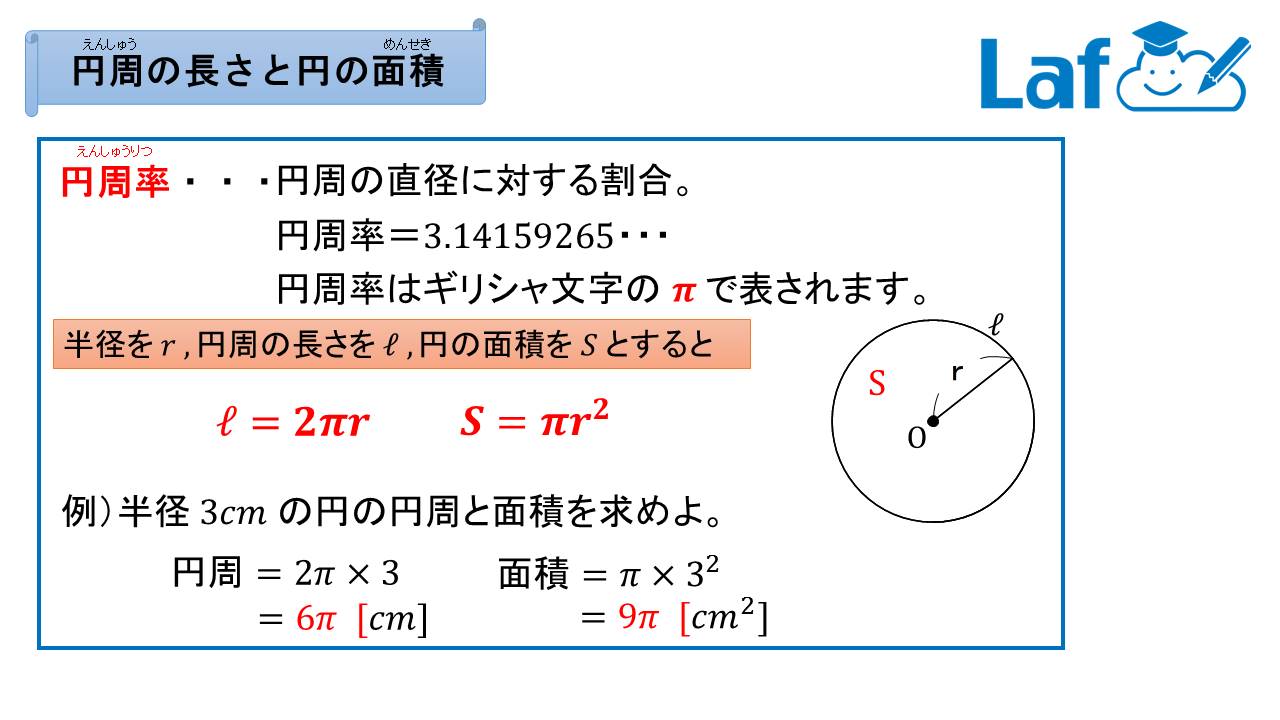
 「微分・積分」の勉強 （1）積分： 以下の問題を考えます。 問題 半径 1 の円の面積Sをπと定義する。 面積S＝π この面積Sを求めよ。 （解答） この問題は、以下の様に解くことができます。 円を、以下の図の様な短冊に分割し、 その円周を積分 ＝ 円の面積 球の表面積を積分 ＝ 球の体積 逆に、 円の面積を微分 ＝ 円周 球の体積を微分 ＝ 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね！ 「積分」は、

円 面積 積分

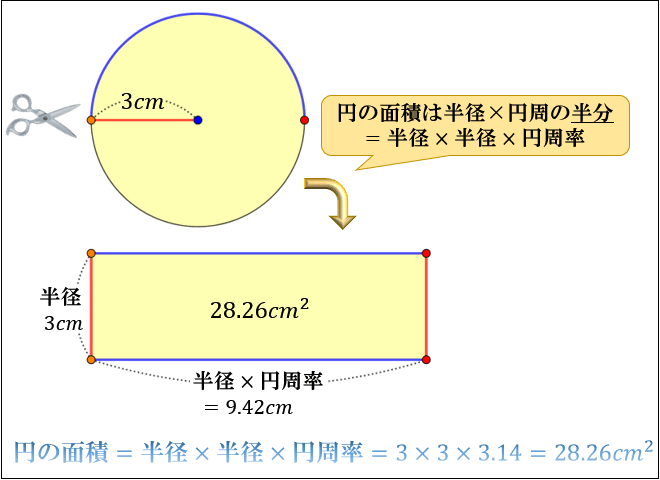
円 面積 積分-なぜ定積分で面積が求まるのか レベル ★ 入試対策 積分 更新日時 面積は「微分の逆の操作」を用いて求めることができる。 一見面積とは無縁な微分という操作の逆を考えることで面積が求められるというのは驚きです。 目次 積分の2通りの 円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。 Tooda Yuuto 「なんで

円周の求め方と円の面積について アタリマエ

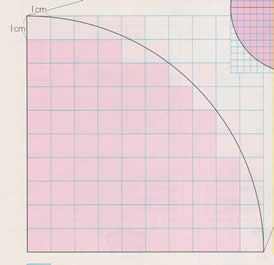
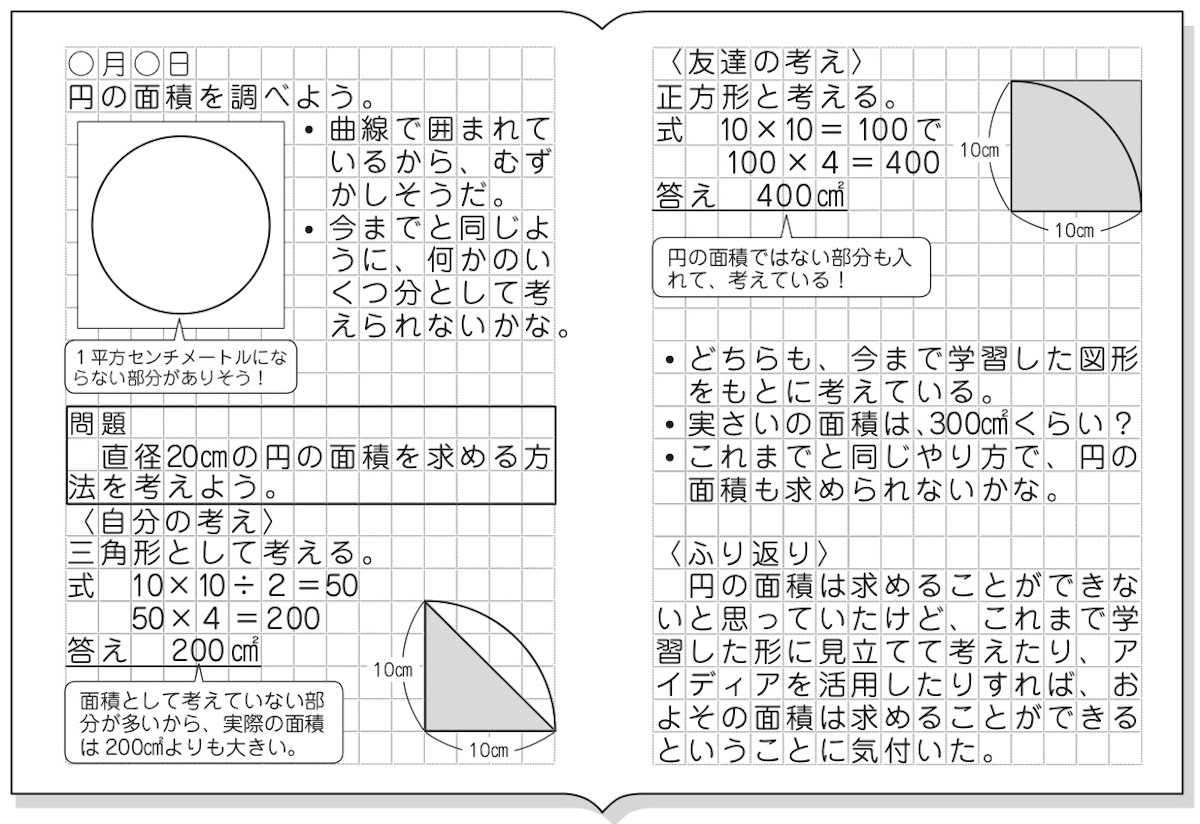
円の面積の初等的な求め方は簡単だ。 でも、そこには積分の初期的な概念がある。 では、その初歩的な概念から積分へはどうやって至るのだろうか。 その積分を身体で感じるために、簡単に求まる円の面積を積分で求めてみよう。高校の数学2や数学3で学ぶ積分は、不定積分ができるものに限って問題が作ら れています。では、不定積分が簡単に求められない場合はどうすればよいのでしょ うか。ここでは面積の計算を通して数値積分のやり方を検討してみましょう。 まず、円の面積を求めることを考えます。楕円の面積を求める方法 楕円とは、円を平たく伸ばしたような二次元図形の一種です。幾何の授業で習った人もいるでしょう。楕円の面積は、長半径と短半径の長ささえわかれば、簡単に求めることができます。 楕円の長半径を特定する 長半径とは、楕円の中心から周上の一番遠い点までの

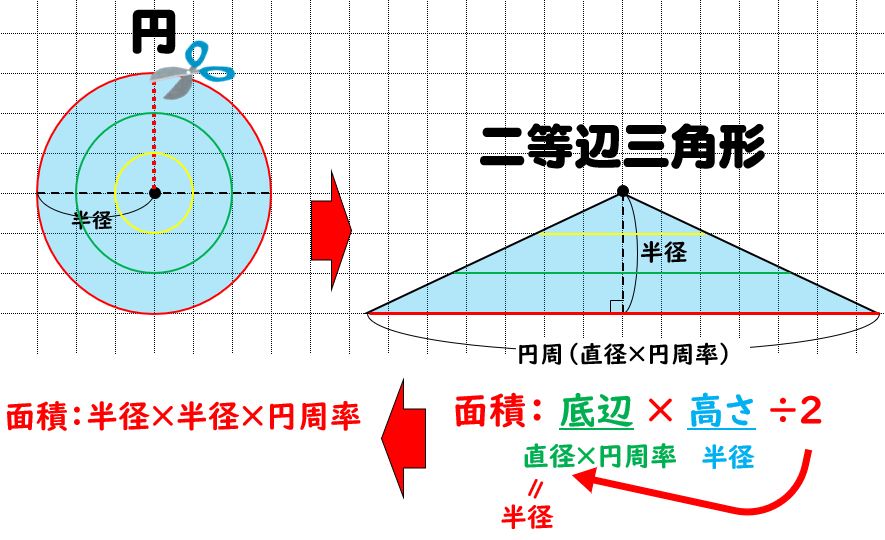
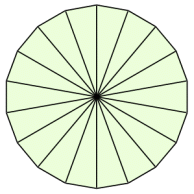
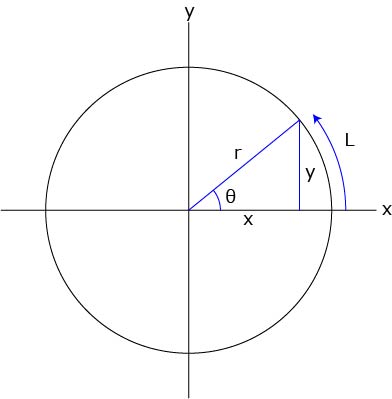
 円の面積を求める方法の1つに、2次元極座標で 方向と 方向の格子に分割して、 を計算する方法がありますよね。 この場合、積分する微小領域の形を縦と横が と の長方形とみなして、その積 をその面積としていると見なせます。 しかし微小領域は厳密に さらに、それぞれの円の扇形から三角形を引いたものを足せば赤色の面積が求められることが見えます。 図のように角度θ1、θ2を置くと、 s = ((円o1の角度θ1扇形の面積) (円o2の角度θ2扇形の面積) (三角形ao1o2の面積)) * 2 と求められます。 円を扇形に切って並べ直してみると 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるの

円 面積 積分のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	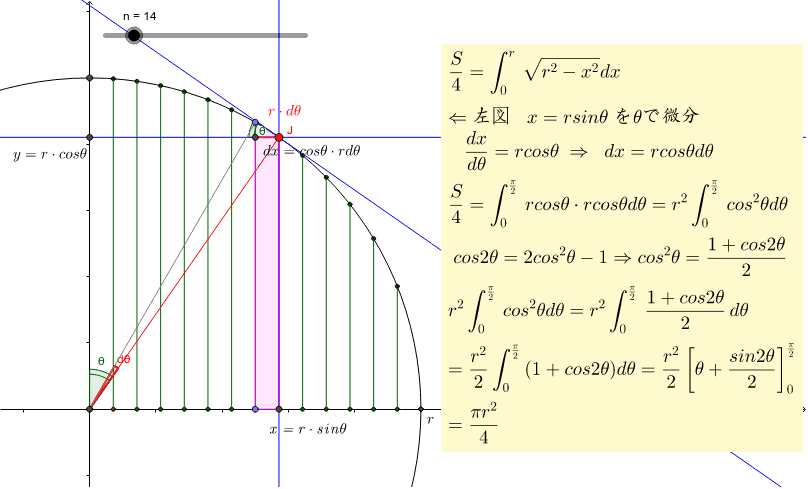円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張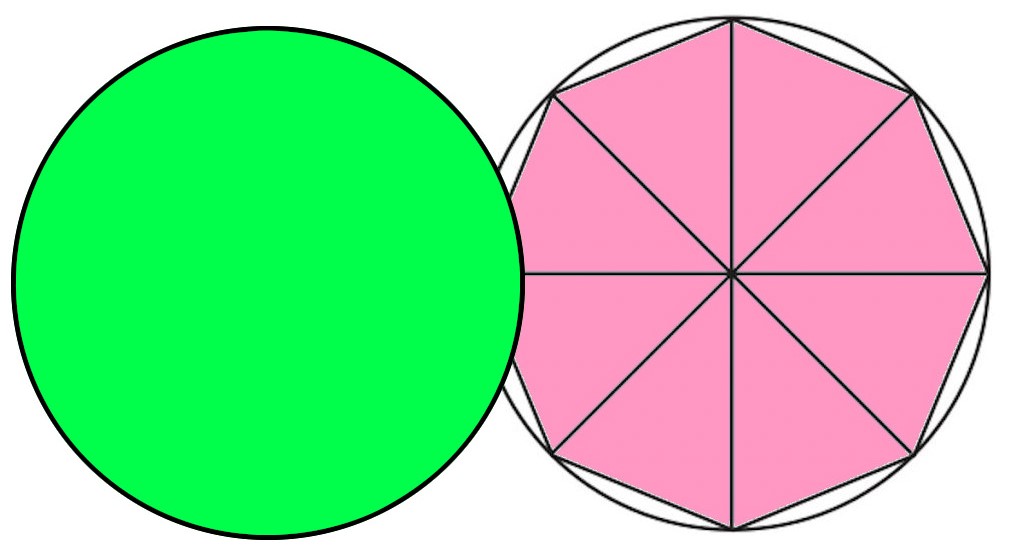
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	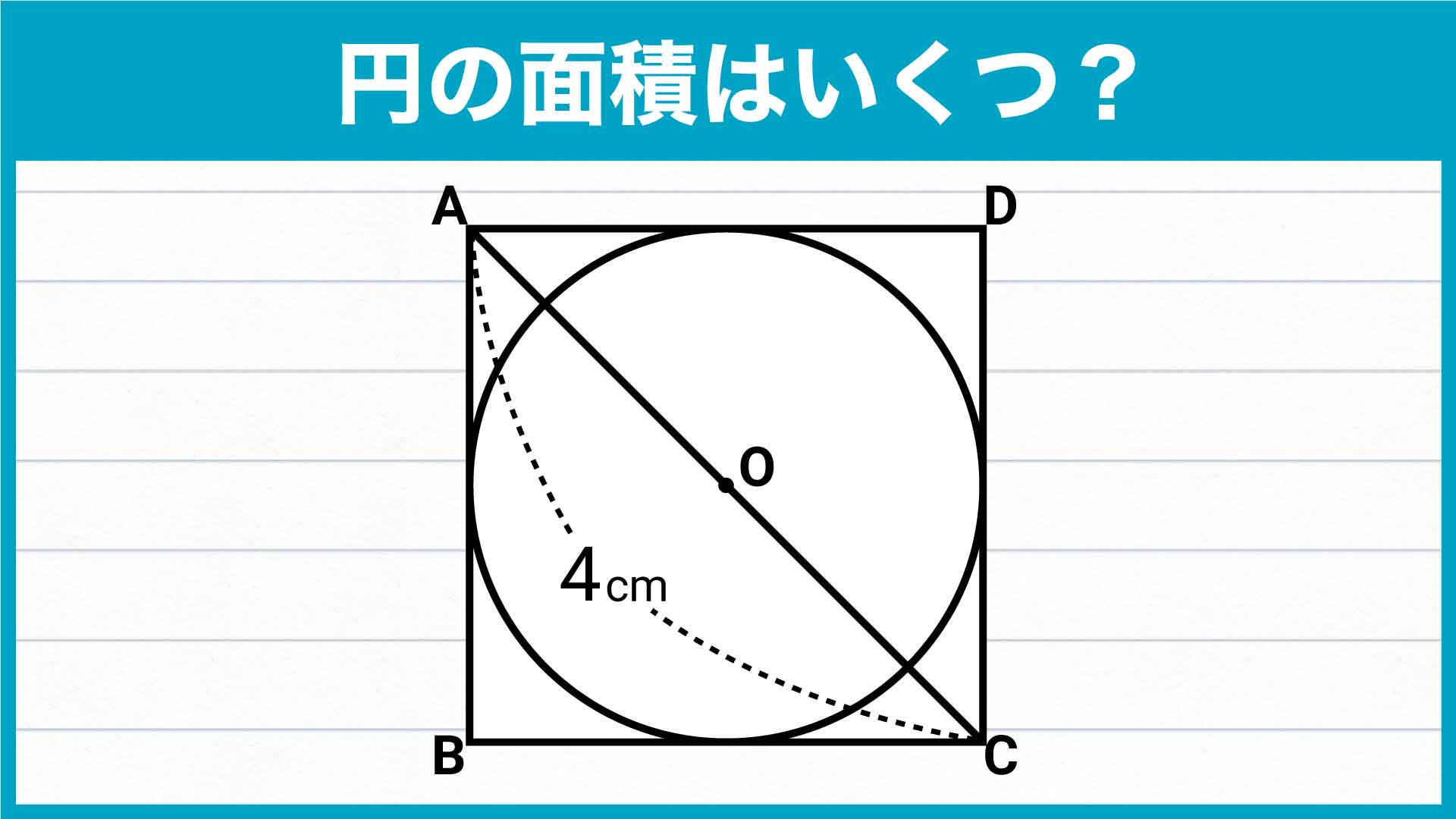円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	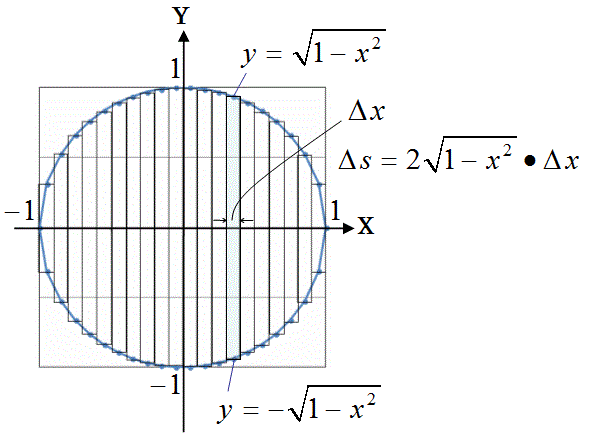円の面積４ 円の面積を求める別の方法 身勝手な主張	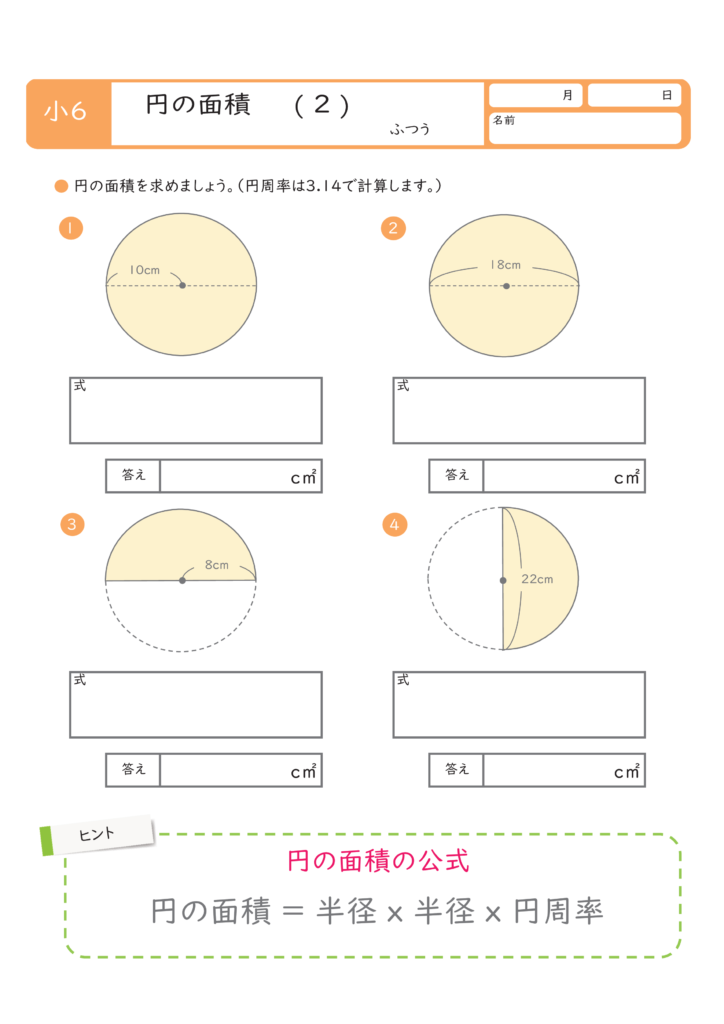円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	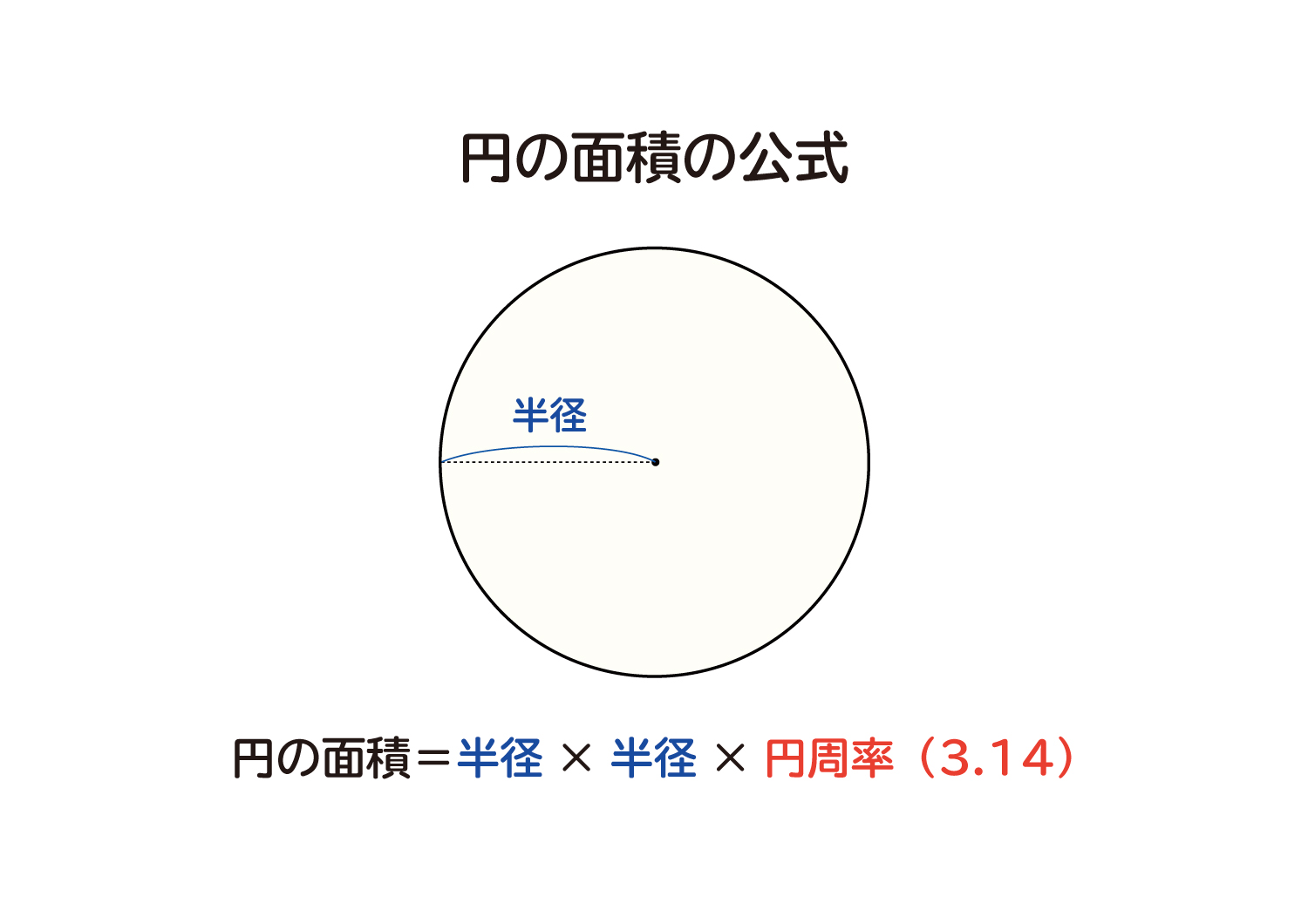円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	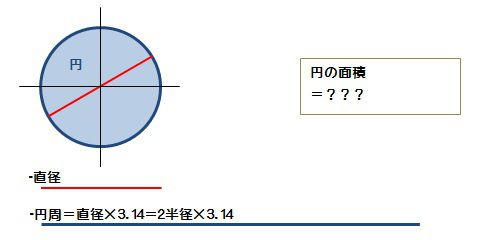円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	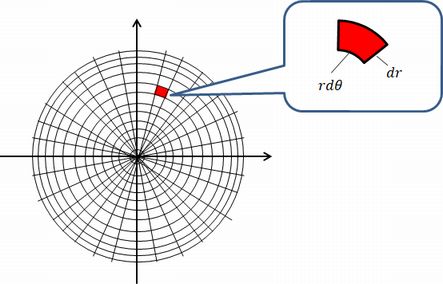円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	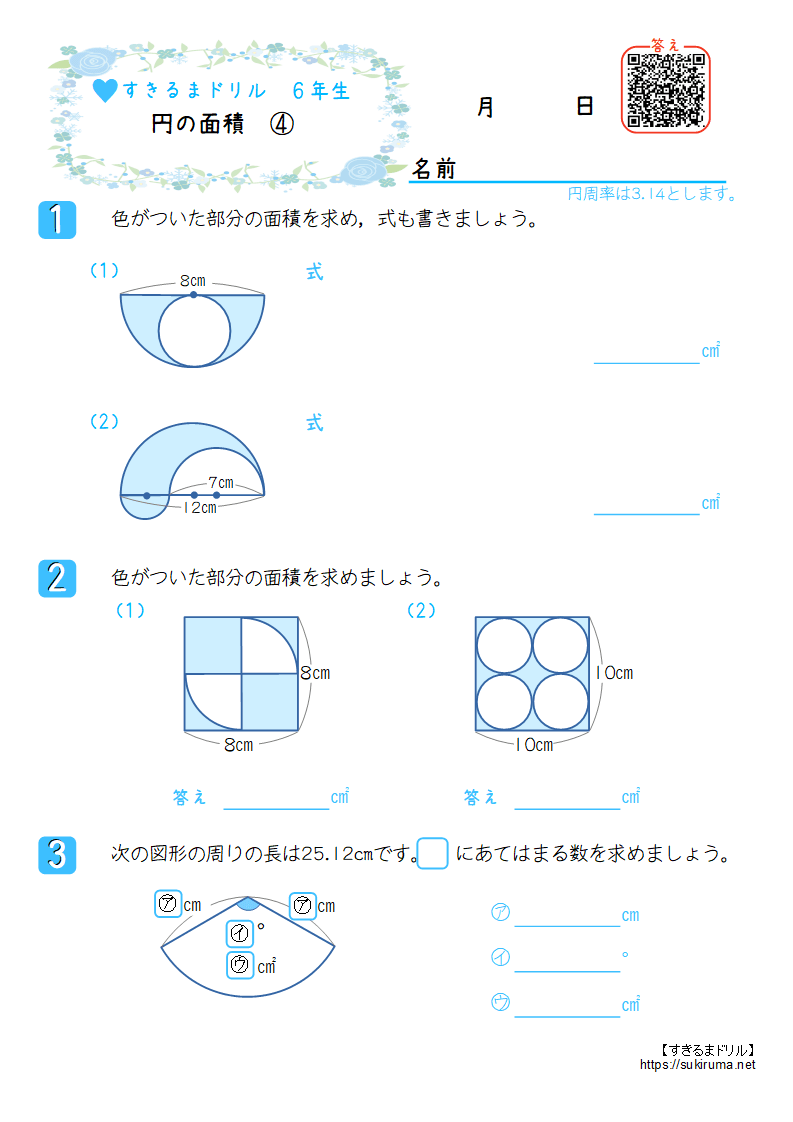円の面積４ 円の面積を求める別の方法 身勝手な主張
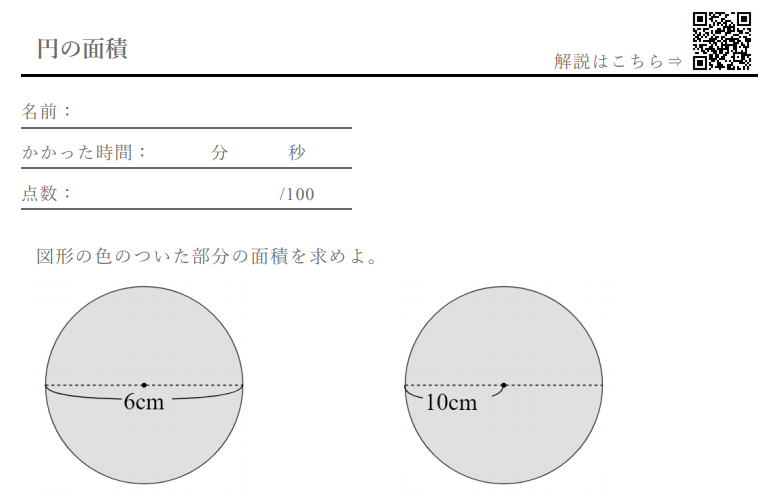円の面積４ 円の面積を求める別の方法 身勝手な主張	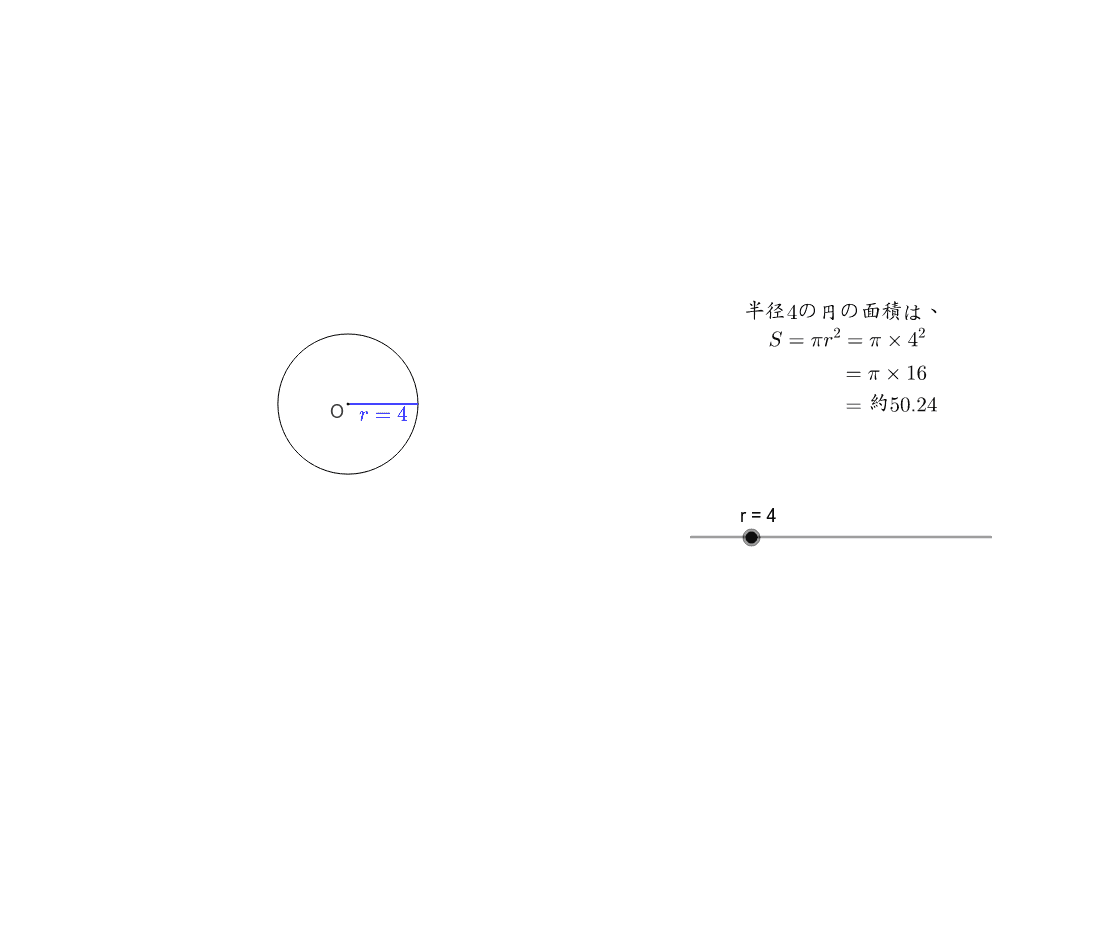円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	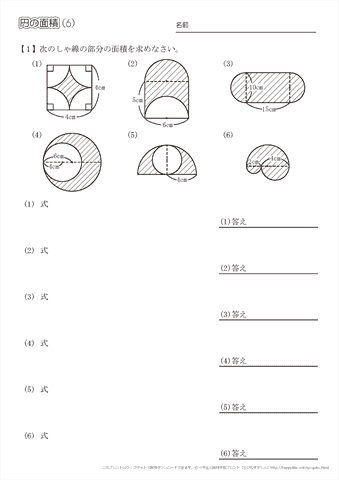円の面積４ 円の面積を求める別の方法 身勝手な主張	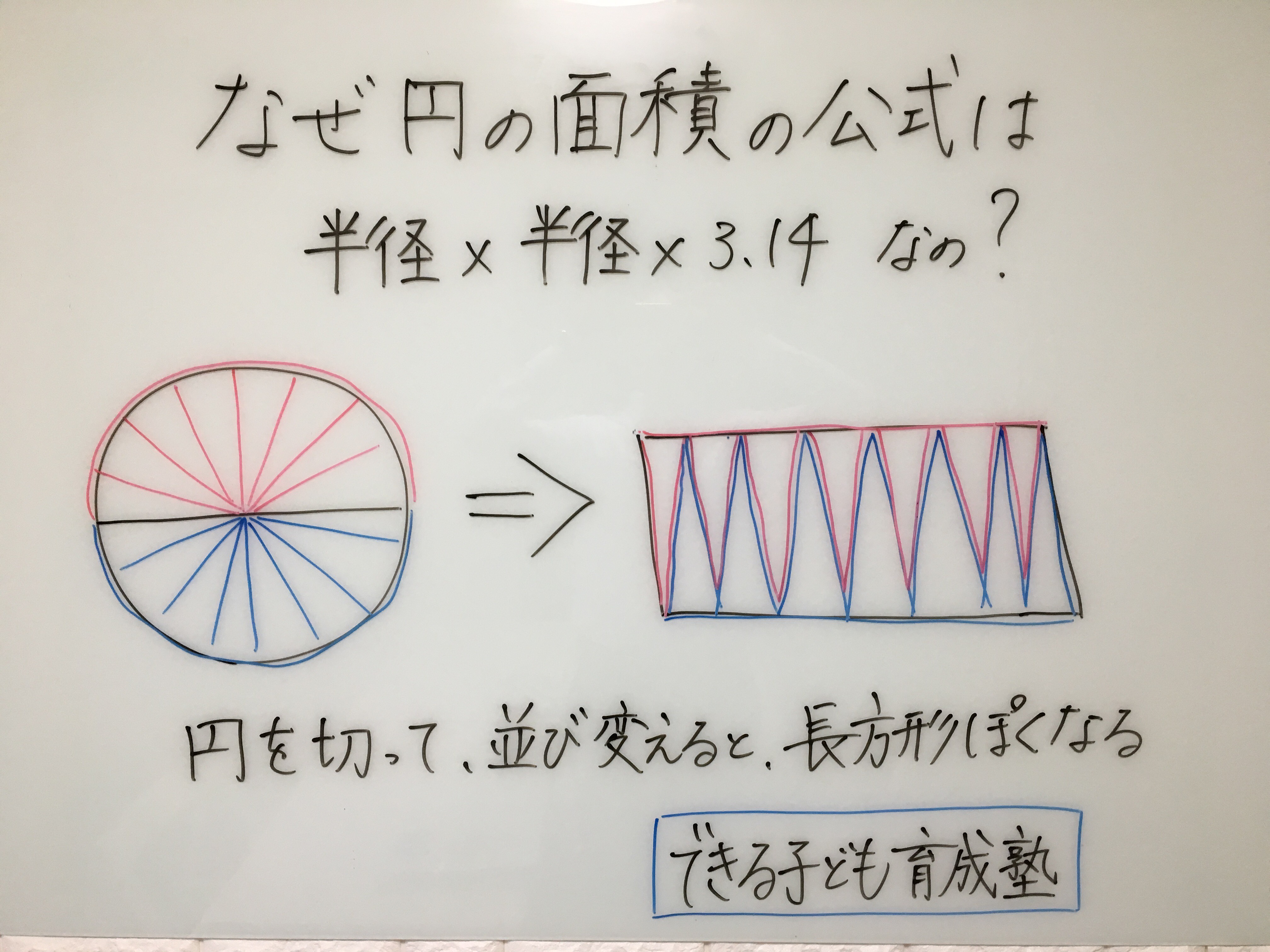円の面積４ 円の面積を求める別の方法 身勝手な主張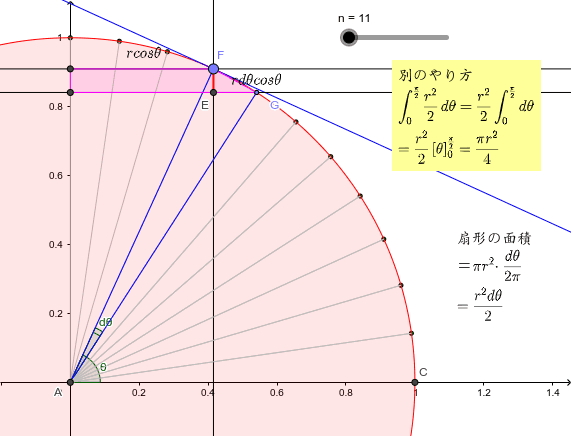
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張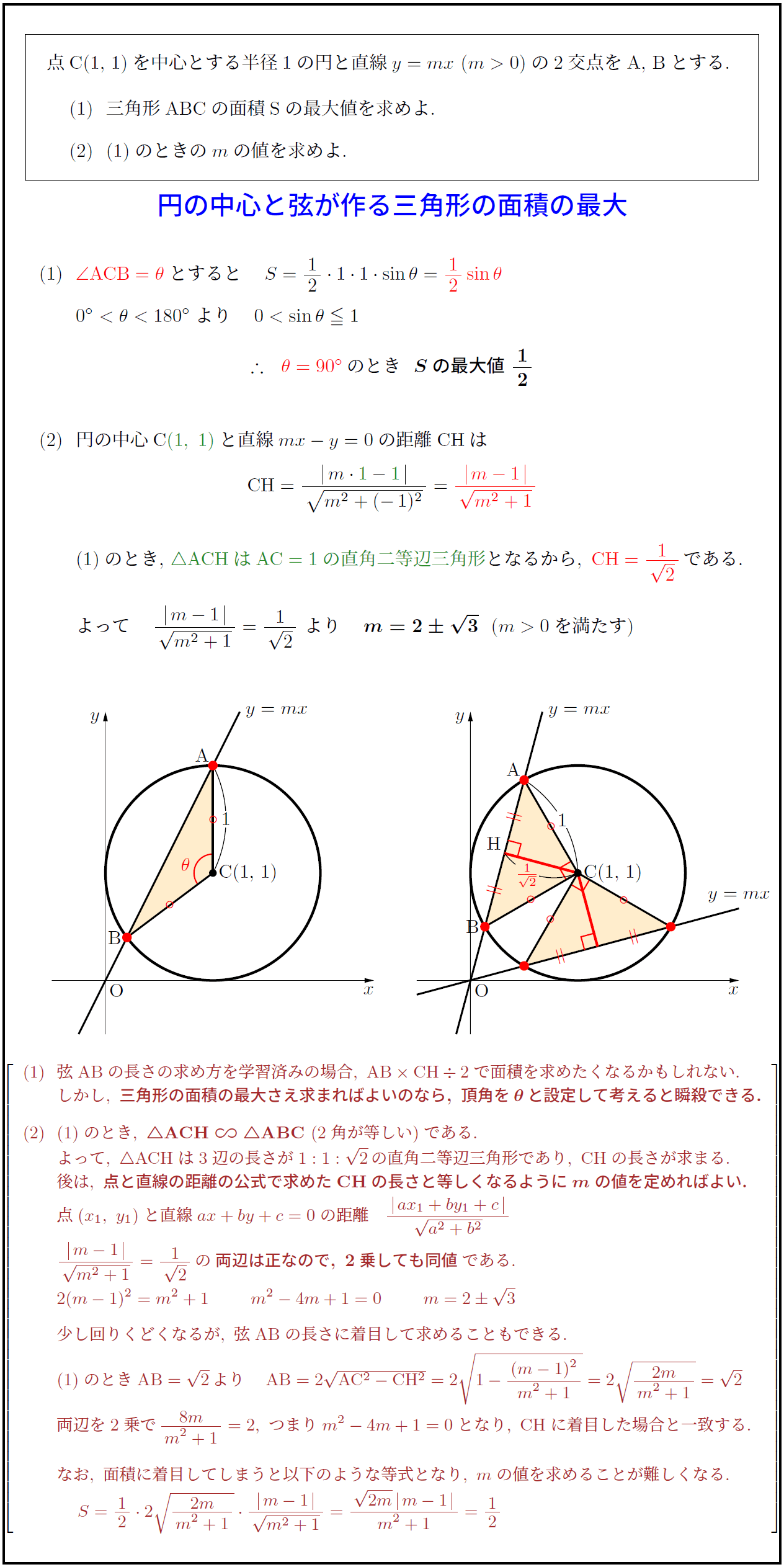
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	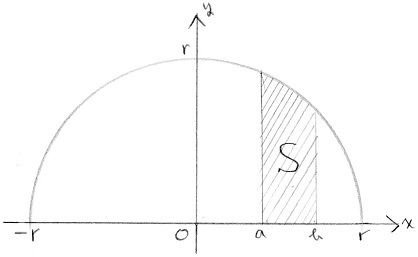円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	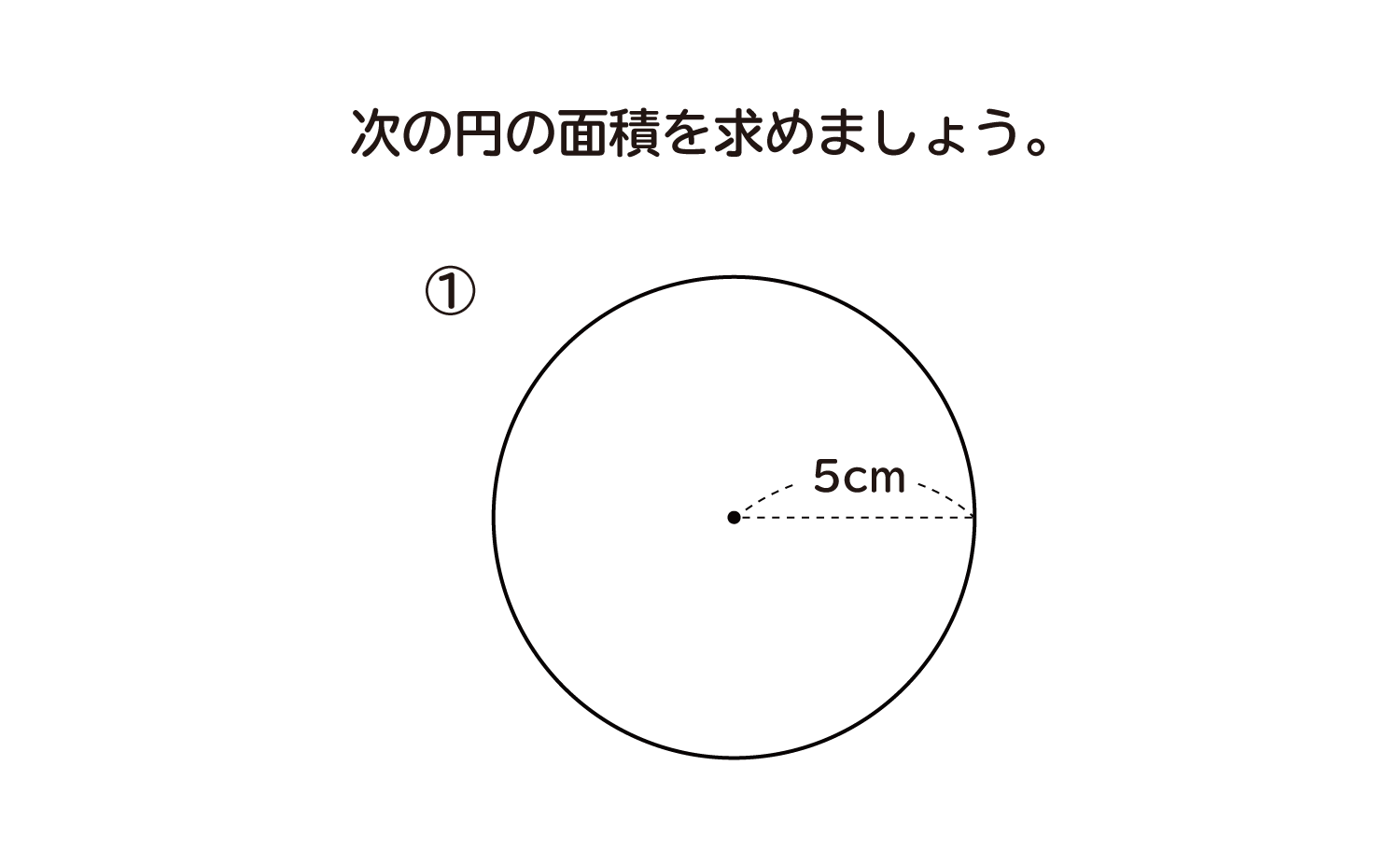円の面積４ 円の面積を求める別の方法 身勝手な主張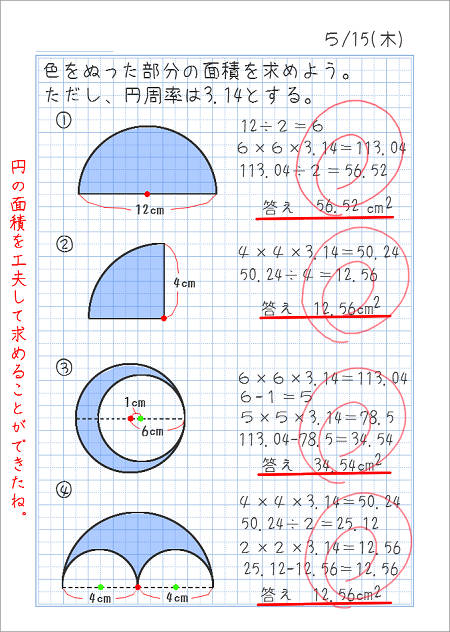
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	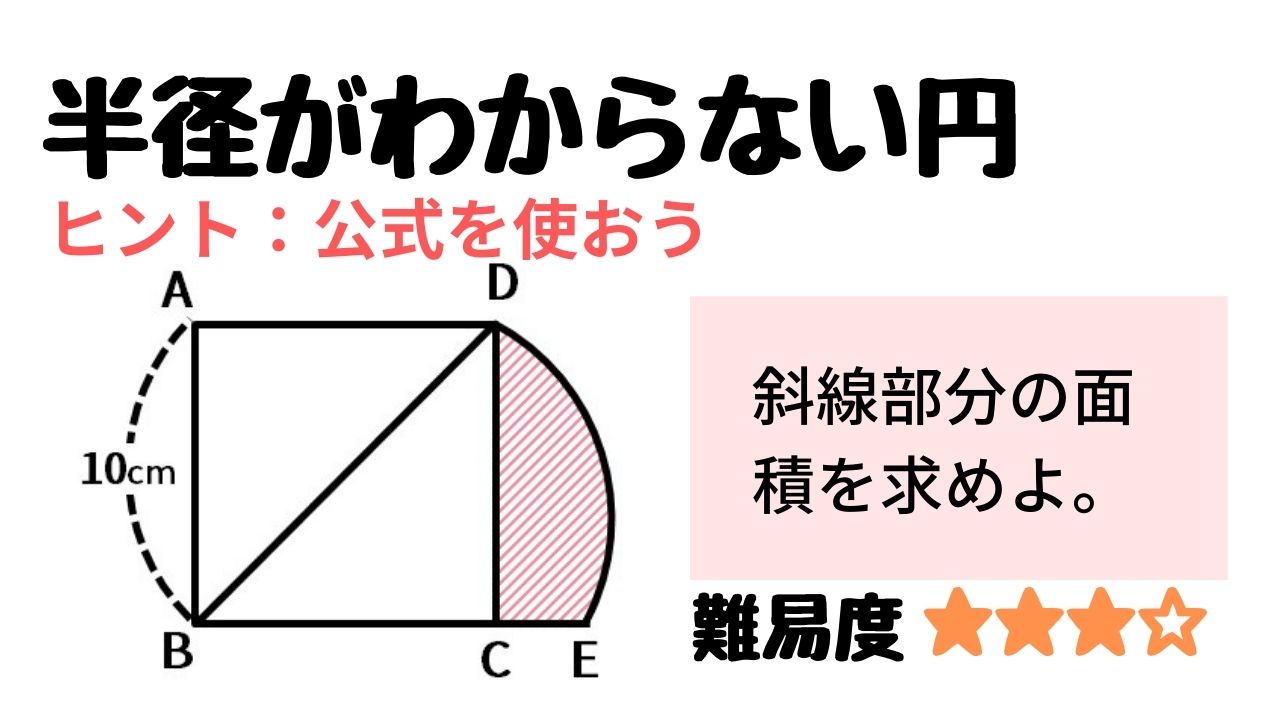円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	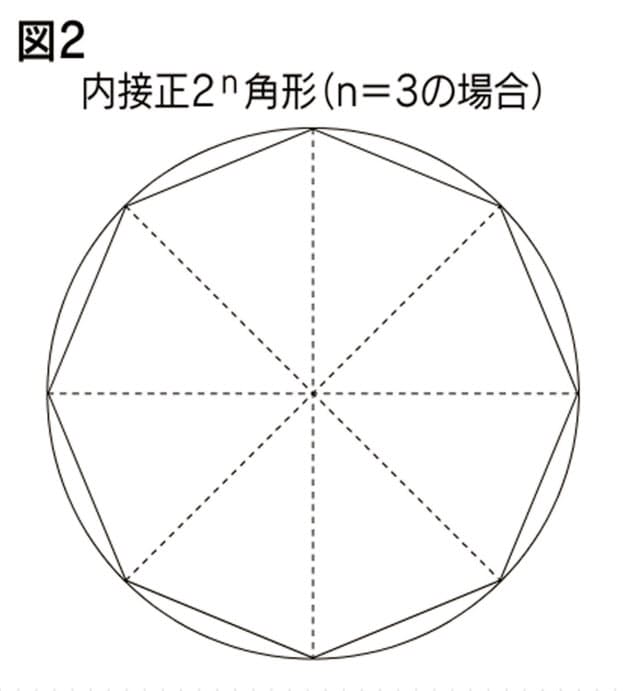円の面積４ 円の面積を求める別の方法 身勝手な主張
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張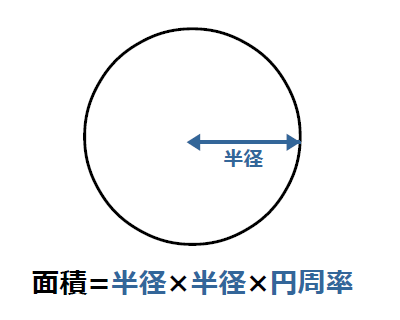
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張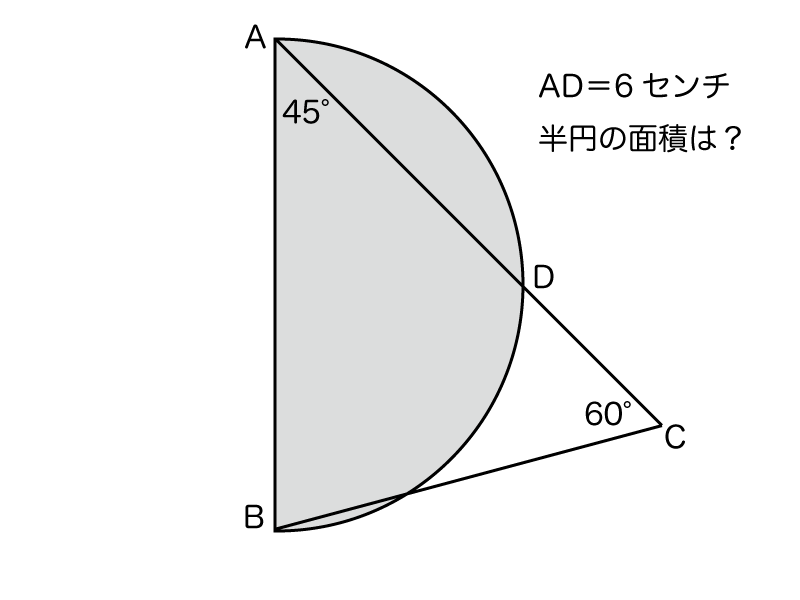
円の面積４ 円の面積を求める別の方法 身勝手な主張	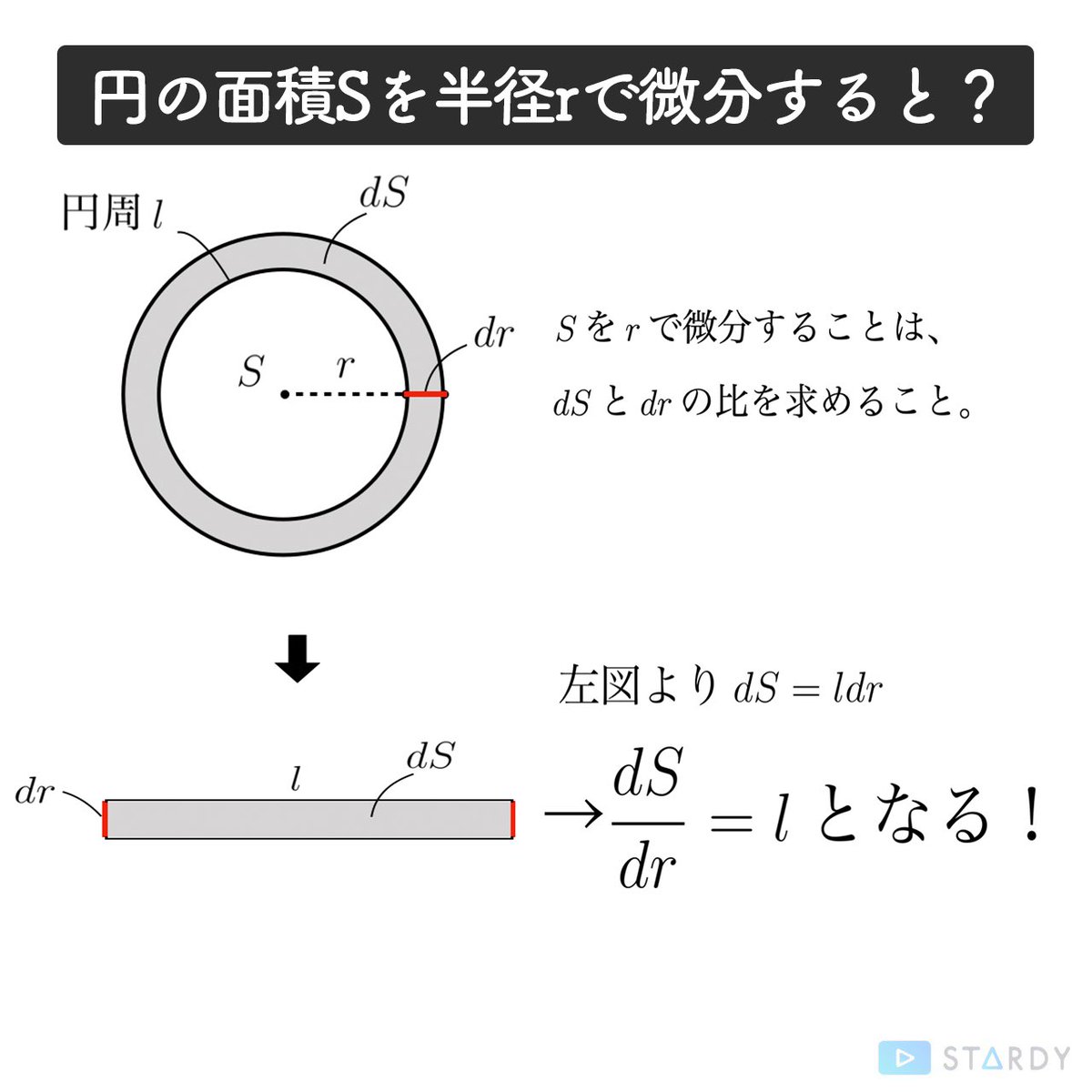円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張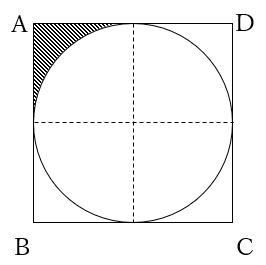
円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張	円の面積４ 円の面積を求める別の方法 身勝手な主張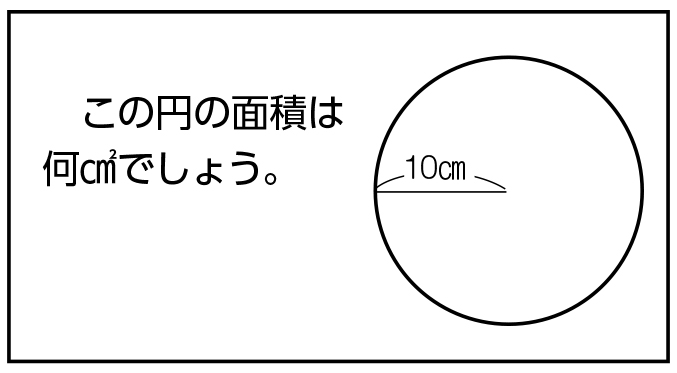
円の面積４ 円の面積を求める別の方法 身勝手な主張	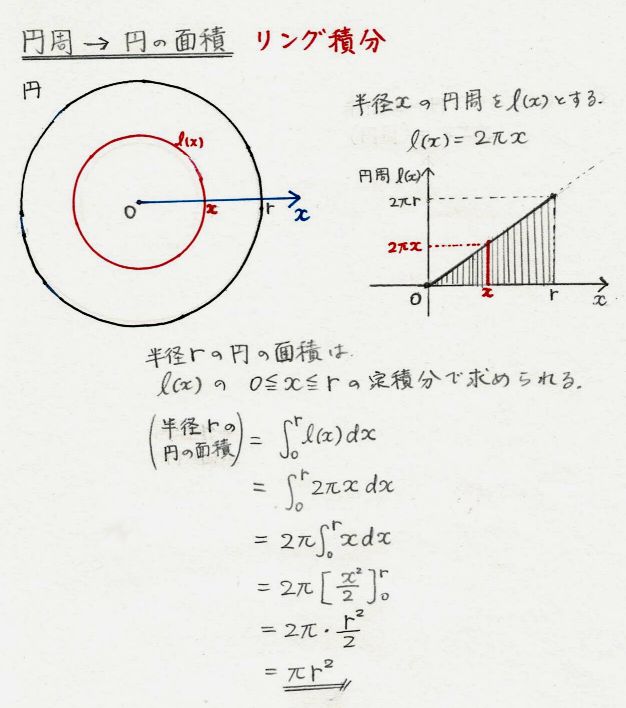円の面積４ 円の面積を求める別の方法 身勝手な主張

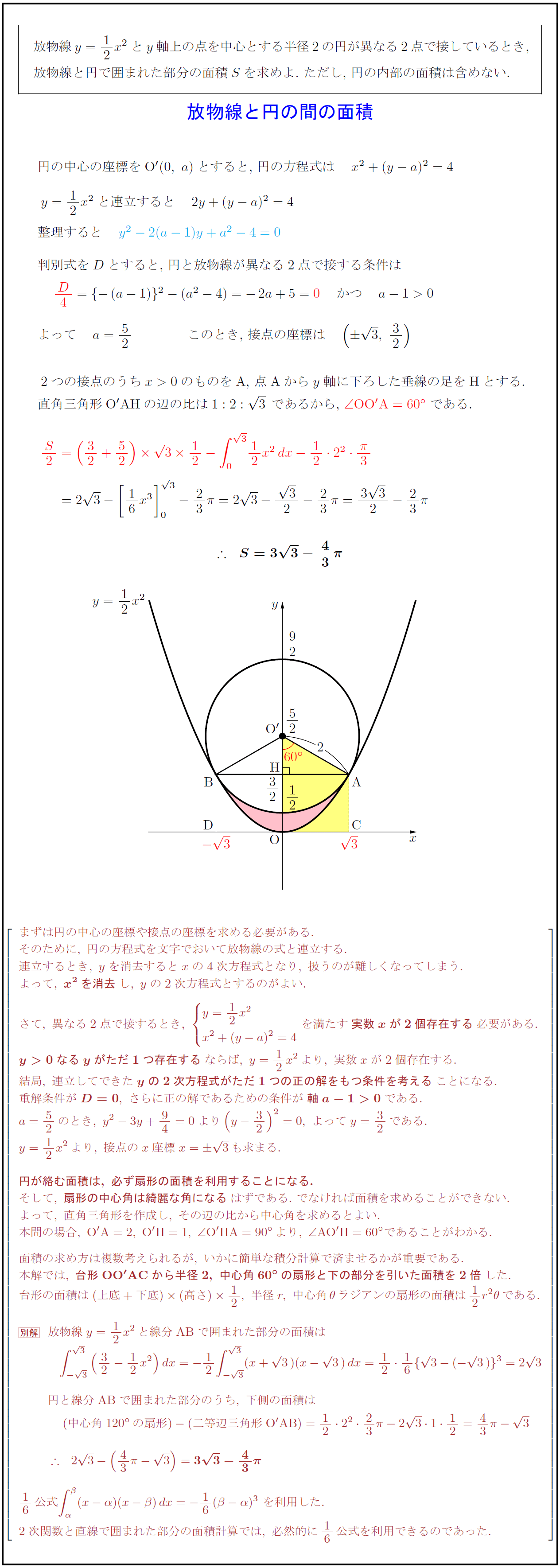
 円の面積、球の体積の公式の微積による証明（導出） そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式まずは公式を書いておきます。半径を \(r\) として\(V=\displaystyle\frac{4}{3}\p円に内接する四角形の面積（4辺から） 四角形の面積（4辺と対角の和から） 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積（中心角から） 弓形の面積（弓形の半径と高さから） 弓形の面積（弓形の弦長と高さ